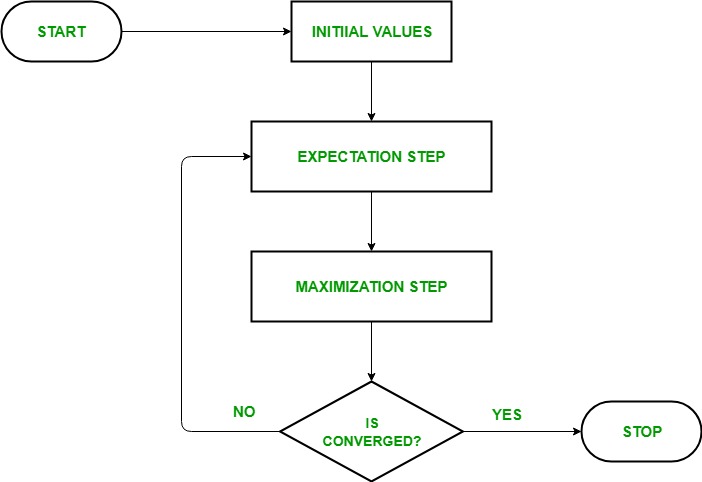
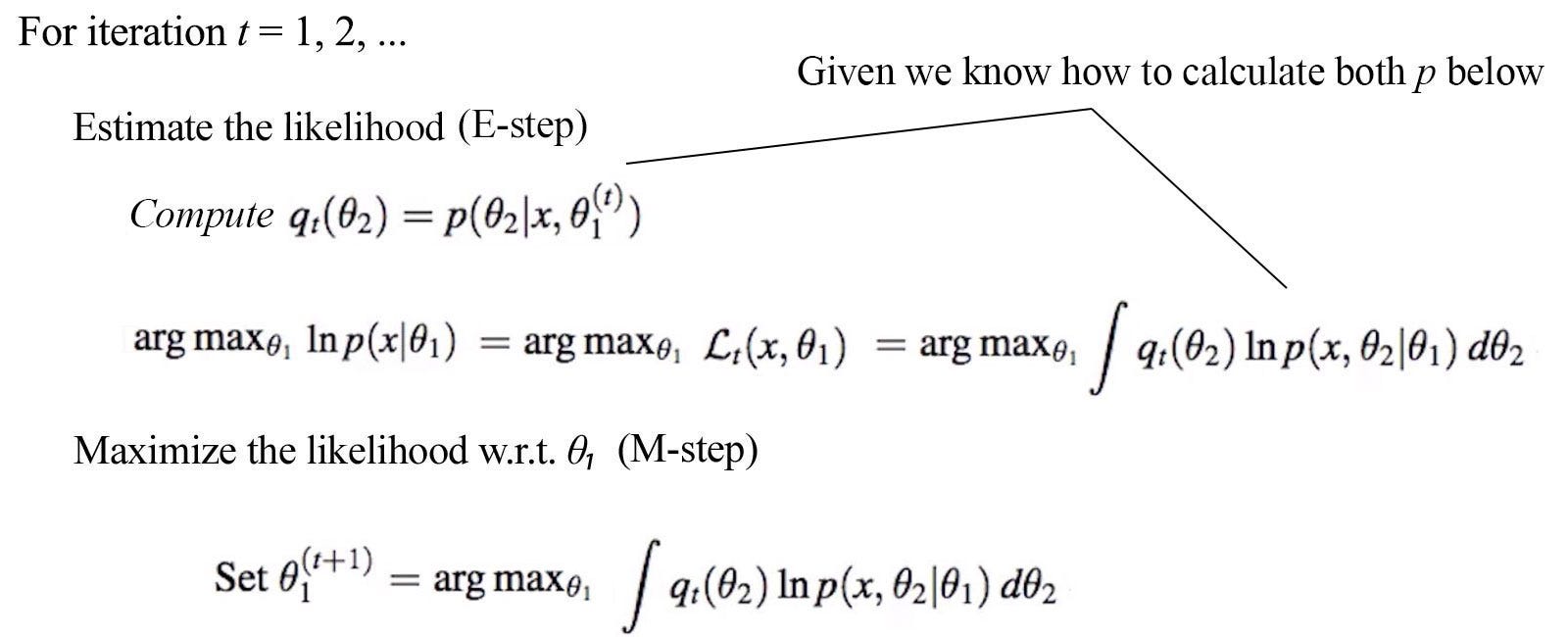Unique Em Algorithm Steps
Ml Expectation Maximization Algorithm Geeksforgeeks Physical Chemistry Formulas Chemical Equation Of Anaerobic Respiration In Animals
Flowchart Showing The Steps Of Em Algorithm Download Scientific Diagram Ray Optics Class 12 Notes Ppt Balancing Equations Worksheet Grade 10 Answer Key
The Em Algorithm Summary Steps Of Download Scientific Diagram Physics Class 10 All Formulas Pdf Edexcel Formula Booklet A Level
An Em Algorithm For The Estimation Of Gmcm Parameters Step 1 Computes Download Scientific Diagram 1d Kinematics Formulas Chemical Word Equations Worksheet
Ml Expectation Maximization Algorithm Geeksforgeeks Class 9 Physics Chapter 1 Motion All Formulas Ap Reference Table 2020
Expectation Maximization Explained By Ravi Charan Towards Data Science Nesa Chemistry Sheet Solid State Questions Answers Pdf
These two steps are repeated as necessary.
Em algorithm steps. More generally however the EM algorithm can also be applied when there is latent ie. This is achieved for M-step optimization can be done efficiently in most cases E-step is usually the more expensive step It does not fill in the missing data x with hard values but finds a. Maximize this simplified Q function in terms of θ.
By the way Do you remember the. The expectation-maximization algorithm is a widely applicable method for iterative computation of maximum likelihood estimates. The EM Algorithm The EM algorithm is used for obtaining maximum likelihood estimates of parameters when some of the data is missing.
Θ_A 06 Θ_B 05 in our example. The K-means algorithm is the most famous variant of this algorithm. Given the parameters θt 1 from the previous iteration evaluate the Q function so that its only in terms of θ.
Each iteration is guaranteed to increase the log-likelihood and the algorithm is guaranteed to converge to a local maximum of the likelihood func-tion. In that case we simply assume that the latent. To summarize the EM loop aims to maximize the expected complete data log-likelihood or auxiliary function Qθ θt 1 in two steps.
EM Algorithm Steps. Generally EM works best when the fraction of missing information is small3 and the dimensionality of the data is not too large. It is worth noting that the two steps in K-means are actually using the idea from EM algorithm.
That is we find. 4 Convex Concave function and Jensens inequality. The algorithm iterates between performing an expectation E step which creates a heuristic of the posterior distribution and the log-likelihood using the current estimate for the parameters and a maximization M step which computes parameters by maximizing the expected log-likelihood from the E step.
Em Algorithm How It Works Youtube Physics Ocr A Level Equation Sheet Balanced For The Rusting Of Iron
Em Algorithm Mathematical Background And Example By Mengsay Loem Towards Data Science Glucoseoxygencarbon Dioxidewaterenergy Equation All Dimensional Formula List Pdf
Expectation Maximization Explained By Ravi Charan Towards Data Science What Is The Chemical Equation For Anaerobic Respiration Balance Practice
What Is Delta In The Maximization Step This Em Algorithm Cross Validated Ocr Alevel Physics Data Sheet Kinematics Problems Worksheet With Answers Pdf
What Is Expectation Maximization Algorithm In Machine Learning Em Tutorial Ap Physics Sheet Relative Density Dimensional Formula
Em Algorithm Archives Top Of The Bell Curve Chemical Formula Aerobic Respiration Ap 1 Physics Equation Sheet
Machine Learning Expectation Maximization Algorithm Em By Jonathan Hui Medium Chemical Equation For Baking Soda And Vinegar Reaction Balanced Combustion Of Methane
Machine Learning Expectation Maximization Algorithm Em By Jonathan Hui Medium Wjec A Level Maths Formula Booklet Reddit Ap Physics 1 Cheat Sheet
